勾股定理2

以下为《勾股定理2》的无排版文字预览，完整格式请下载

下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。

勾股定理淅川上集一中 王某某勾股定理（gou-gutheorem)

直角三角形两直角边的平方和等于斜边的平方。如果直角三角形两直角边分别为

a、b,斜边为c，那么出示导纲，学生自学阅读课本110-111面，大家自己动手拼一拼，做一做1、准备四个全等的直角三角形（设直角三角形的两条直角边分别为a，b，斜边为c）；你能用这四个直角三角形拼成一个以斜边c为边的正方形吗？拼一拼试试看? 你能否就你拼出的图说明a2+b2=c2。

2.拼图14.1.5请试一试，写出完整的证明过程。展示评价分工∵ c2= 4?ab/2 +(b-a)2 =2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ；

也可以表示为c24?ab/2+(b- a)2

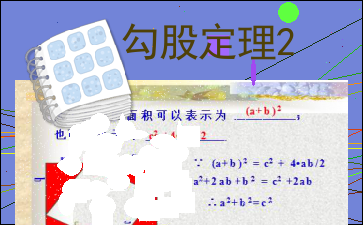
∵ (a+b)2 = c2 + 4?ab/2a2+2ab+b2 = c2 +2ab∴a2+b2=c2大正方形的面积可以表示为 ；

也可以表示为(a+b)2c2 +4?ab/2展示评价分工 如图，为了求出位于湖两岸的两点A、 B之间的距离，一个观测者在点C设桩，使三角形ＡＢＣ恰好为直角三角形．通过测量，得到AC长160米，ＢＣ长128米．问从点A穿过湖到点B有多远?在直角三角形ＡＢＣ中，

AC＝１６０米，　ＢＣ＝１２８米，

根据勾股定理可得

ＡＢ＝

＝

＝96（米）．

答： 从点A穿过湖到点B有96米．解例质疑解难你能从上面两个图形中找到其他证明勾股定理的方法吗？

你能自己画一个图形来证明勾股定理吗？导学归纳通过本节课的学习，你学到了哪些知识？

你还有什么疑问吗？二填空题 1.在? ABC中,∠C=90°, (1)若c=10,a:b=3:4,则a=____,b=__ 8 _. (2)若a=9,b=40,则c=______. 2.在? ABC中, ∠C=90°,若AC=6,CB=8,则?ABC面积为___,斜边为上的高为____. 拓展训练： 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( )

2.Rt? ABC的a=6,b=8,则c=10 ( ) ?641?244.8如图，求等腰三角形ABC的面积 。ABC131310D解：作高AD，

则BD=DC=5作业:

1:112 面 1.2

2:补充作业：如图在△ABC中，∠ACB=90o， CD⊥AB，D为垂足，AC=3cm,BC=4cm.

求① △ABC的面积；

②斜边AB的长；

③斜边AB上的高CD的长。思考题ACOBD 一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?再见

[全文已结束，注意以上仅为全文的文字预览，不包含图片和表格以及排版]

以上为《勾股定理2》的无排版文字预览，完整格式请下载

下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。