第三章 根的分布

以下为《第三章 根的分布》的无排版文字预览，完整格式请下载

下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。

第三章XXXXX3.3二次函数第二课时方程根的分布问题

本节目标：

1.一元二次方程根的分布，体会数形结合的数学思想；

2.从韦达定理到数形结合方法转变研究方程根的分布。

复习回顾：

1、若关于x的一元二次方程 的一根大于零、另一根小于零，求实数a的取值范围．

2、一元二次方程 有两个实根，一个比3大，一个比3小，求的取值范围。

探究与发现：

例1.已知方程 有两个负根，求m的取值范围。

问题1　解决一元二次方程根的问题能否借助函数图像，画图分析。

问题2　 图中的哪些因素影响根的大小?

问题3　 写出例题1的条件

例2．求实数m的范围，使关于x的方程 有两个实根，且满足 。

画图分析，写出题目条件。

例3．若关于x的方程 有两相异实根，且两根均在区间[0,2]上，求实数 的取值范围．

画图分析，写出题目条件。

小结

一般地，用函数思想结合图象来分析方程 的实根分布情况要考虑四个必要条件。①二次项系数a，决定图象开口（延伸）方向；②判别式 决定与x轴的位置；③对称轴 ，决定图象左右平移；④特殊点（区间端点）所对函数值 的正负，决定图象开口大小。

一元二次方程 根的分布情况

设方程 的不等两根为 且 ，相应的二次函数为 ，方程的根即为二次函数图像与x轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）

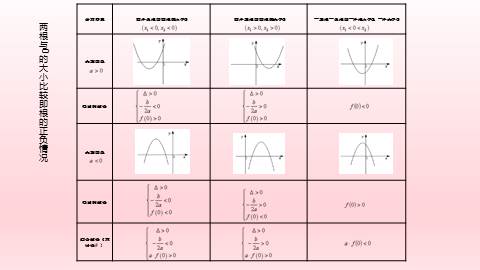
两根与0的大小比较即根的正负情况

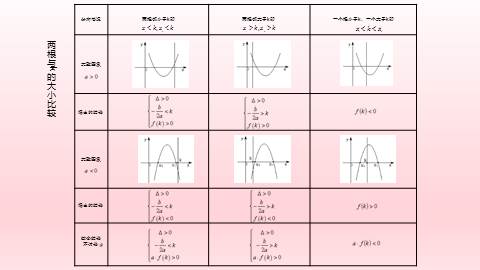
两根与k的大小比较

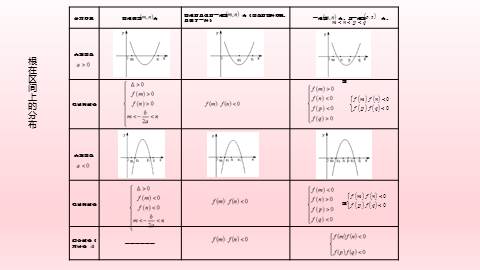
根在区间上的分布

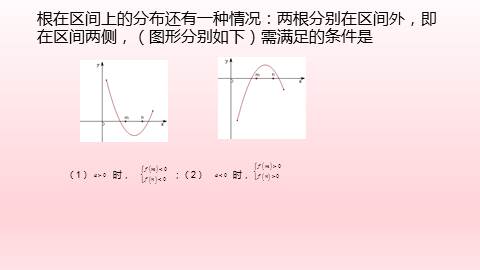
根在区间上的分布还有一种情况：两根分别在区间外，即在区间两侧，（图形分别如下）需满足的条件是

（1） 时， ；（2） 时，[全文已结束，注意以上仅为全文的文字预览，不包含图片和表格以及排版]

以上为《第三章 根的分布》的无排版文字预览，完整格式请下载

下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。